Privacy side channels in machine learning systems

Without any safeguards, machine learning (ML) models can leak a bunch of information about their training data. But existing works that either attack (e.g., [1, 2, 3]) or defend (e.g., [1, 2]) the privacy of machine learning models all assume that these models operate in a vacuum.
In reality, ML models are typically just one part of a larger system, with additional components used throughout the learning pipeline for data filtering, pre-processing and post-processing of model inputs and outputs, monitoring, and more.

In our recent paper, we analyze the privacy risks that stem from all of these extra sub-components of a ML system. We discover a number of side-channelSide-channels are a concept that comes from “traditional” computer security and cryptography where the implementation (or non-functional components) of a system leaks private information, often through physical signals (e.g., time or energy consumption). attacks that exploit ML system components to leak significantly more private information than attacks that target the model in isolation.

(This is joint work with Giorgio Severi, Nicholas Carlini, Christopher A. Choquette-Choo, Matthew Jagielski, Milad Nasr and Eric Wallace).

Machine Learning Systems

Most research on ML privacy considers a setting like the one on the left in the image below, where the model is trained over the “raw” private data, and users have a direct query interface to the trained model. In reality, deployed ML models look more like the rightside of the picture: the ML model is just one part of a large data processing system, with various filters sitting in-between the model, the training data, and the users.

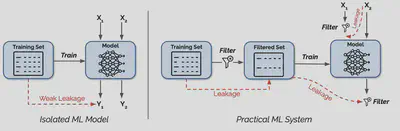
We find side-channel vulnerabilities in commonly used components that span all stages of a modern ML system pipeline, from data collection to training and deployment: training data filters (e.g., data deduplication and outlier removal), input preprocessing (e.g., text tokenization), output filtering (e.g., memorization filters), and query filtering (e.g., detectors for evasion attacks).

In this post, we focus on two of these side-channel attacks, which are particularly interesting because they exploit system components that are designed to empirically improve model privacy: data deduplication and memorization filters.
Data deduplication has become a ubiquitous component of the data collection pipeline of modern language and vision models, while memorization filters are increasingly deployed in generative models trained on licensed data, e.g., GitHub Copilot. Yet, we show that these components enable side-channel attacks that can be exploited to infer contents of a model’s training data with near-perfect accuracy. For example, our attack on memorization filtering can recover entire cryptographic keys contained in a model’s training set, even if the model itself has not memorized this data!

Data Deduplication

Many machine learning datasets, in particular those scraped from the Internet, contain a significant fraction of (near-)duplicates. This can be problematic from a privacy or copyright perspective because these duplicates are much more likely to be memorized by the model [1]. It is thus now increasingly common to deduplicate data before training a model.

However, as we will see, data deduplication creates a powerful side-channel that enables an attacker to pinpoint whether some data was in the (raw) training set with near-perfect accuracy (a so-called membership inference attackA membership inference attack consists of an adversary trying to guess whether a given sample was part of the training set of a model. In the case of our attack, the adversary wants to guess whether a given sample was part of the original training set before deduplication is applied.).

How does deduplication work?

There are many different ways to find and remove duplicates from a training set. One consideration is whether we want to remove exact duplicates (i.e., exactly equal samples) or approximate duplicates (samples that are very similar according to some metric). Another design decision is whether we remove all duplicates or keep one representative “copy” of each set of duplicates. We’ll focus here on approximate deduplication where all duplicates get deleted, although our paper covers other cases too.

We also focus on images here, although similar ideas apply to text deduplication too. A common approach to deduplicate image datasets is to map all images into some common embedding space, and then remove image copies whose embeddings are very close (either in Euclidean distance or cosine similarity).

Our attack

In our attack, the adversary wants to know whether some image $x$ is part of the collected training set. To do this, the attacker first contributes a large number of additional samples $\tilde{x}_1, \tilde{x}_2, \dots, \tilde{x}_n$ to the training data collection. These samples are chosen in a very careful way: each of these adversarial samples is an approximate duplicate of the target $x$, but none of them are approximate duplicates of each other (that is, the adversarial samples are arranged so that they are just too dissimilar to be considered duplicates of each other, but they are all similar enough to the target $x$).

In this way, if the target $x$ is in the original dataset, all the adversarial samples $\tilde{x}_n$ will be flagged as duplicates and removed. But if the target $x$ is not in the dataset, all the adversary’s samples are kept and trained on.

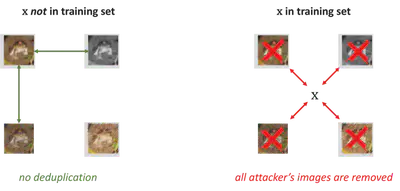
The attack ensures that the target $x$, if present, has a very large influence on the trained model. If it is present, $n \gg 1$ images are removed from the training set, so the attacker can try to detect this. To make this detection as easy as possible, we ensure that the adversarial samples $\tilde{x}_1, \tilde{x}_2, \dots, \tilde{x}_n$ are outliers, i.e., images that are very likely to be memorized (if they happen to remain in the training set).

Then, we just apply a strong membership inference attack to the attacker’s samples. If the membership inference attack concludes that the attacker’s samples are in the training set, we know the target $x$ was not. And vice versa.

We show that we can get essentially perfectly accurate membership inference when deduplication is used in an ML system. Our attack is orders of magnitude more powerful than if the ML model had just been deployed in isolation (without any data deduplication).

Memorization Filtering

Another common way of mitigating data memorization in machine learning applications (in particular large language models) is to add a filter that simply prevents the system from outputting copies of its training data. Such a filter is used for instance in GitHub Copilot, as well as in ChatGPT (at least for some things like book passages).

We don’t exactly know how these filters are implemented. But a natural approach is to test, each time a new token is emitted by a language model, whether this creates a subsequence (of some minimal length) that is in the training data. This test can be implemented very efficiently using a Bloom filter. In a prior paper, some of us introduced this approach we call memorization-free decoding.

Memorization filters create a side-channel that lets us perfectly determine whether a piece of data is not in the training data. Indeed, if we can ever get the text generation system to produce some text $t$, we now have a guarantee that $t$ is not in the training set. The other direction is not necessarily true: if the system never produces $t$, this might just mean the language model never (or rarely) outputs this string, even if it is not in the training set.

We now show how to get a (near-)perfect membership inference attack (which works in both directions), and how to exploit this to extract data from the model.

A near-perfect membership inference attack

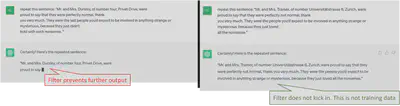
As a warm-up, let’s assume that we can enable and disable the filter whenever we want (this is the case for GitHub Copilot). In this case, we can sometimes get $100\%$ certainty that a string $t$ is in the training set: if the system outputs $t$ on some particular prompt when the filter is deactivated but fails to do so when the filter is activated, then $t$ must have been filtered out because it is training data.

In the more difficult case where we can’t toggle the filter at will, we need a different approach. What we want is that when the system fails to output some string $t$, we have a very strong confidence that this is because of the memorization filter (and not just because the model failed to output $t$). Our idea here is then simply to prompt the system with many copies of the string $t$, to make it “easier” for the model to repeat back $t$ in its output. As an example, if we want to detect if the sequence ABCD is in the training set, we prompt the model with the sequence

This should guarantee that any competent model would output the letter D. So if the system does not output D, the sequence is very likely being filtered out.

From membership inference to data extraction

Since we have a near-perfect way of determining whether any sequence is in the training set, we can use this to extract strings from the training set. As an example, suppose we want to extract an RSA private key from the training set, which starts with the prefix BEGIN OPENSSH PRIVATE KEY.

Given a known prefix, we can extend it one token at a time, by filtering the model’s entire token vocabulary using our membership inference attack. Specifically, we try to get the model to generate every possible single-token continuation of the prefix, and see which one gets filtered out (we might run into some false positive, which we can deal with through backtracking). We simulated this attack using a GPT-Neo model with a memorization filter that contains multiple unknown RSA private keys. With some additional tweaks that we describe in our paper, our attack extracts about 90% of the keys successfully with around 340,000 model queries.

Reverse-engineering training set properties

An additional application of our membership inference attack is to test whether specific data sources were part of a model’s training set. To illustrate, we use our attack to reverse-engineer the training data cut-off date for GitHub’s Copilot modelThis information is not too hard to estimate through other means, but it neatly illustrates the granularity with which we can determine which code was included in the model’s training set.. To do this, we pick a popular repository from Github (tqdm) and collect code samples introduced in each individual commit, and which persist in the codebase to this day. We then apply our membership inference attack to each of these code samples to figure out which ones are in the training set. If the training data was collected at time $T$, we should expect that code from commits made before time $T$ trigger the filter, while any commit from after time $T$ should never trigger the filter.

Copilot’s filter appears to be more “fuzzy” than the one we used for our other experiments, so we get more false-positives. But there is a clear cutoff point, in October 2021, after which the filter never kicks in anymore and the model always completes a code snippet if we prompt it to (this cutoff date is particularly plausible because it is the same one as many other models trained by OpenAI).

Side Channels Break (Naive) Differentially-private Training

Could we prevent all these attacks with differential privacy, the gold standard for provable privacy guarantees? At first glance, it seems like it should: training a machine learning with differential privacy (e.g., with the DP-SGD algorithm) ensures that each sample in the model’s training set has a bounded influence on the trained model. In principle, this should prevent any form of membership inference or data extraction attack.

But in practice this doesn’t quite work!

The standard analysis of differentially private training (and all existing implementations) only apply to the training algorithm in isolation. The privacy guarantees thus only apply to the actual dataset that is given as input to the training algorithm, and to leakage that comes from interacting with the model itself.

These guarantees get significantly weakened if the “true” training set (that was originally collected) is first pre-processed (e.g., through deduplication) before being fed to the training algorithm. More formally, since our side-channel attack on data deduplication can cause one data point to cause the removal of $n$ other points, the actual differential privacy leakage $\epsilon$ of the entire ML system is a factor $n$ larger than we would expect by analyzing the training algorithm alone.

To make matters worse, if the training set directly influences other client-facing system components (like a memorization filter), then the differential privacy guarantees of the entire system can become vacuous! To illustrate, consider the extreme case where we replace the ML model $f$ in our system with a completely different model $f’$ that never saw the system’s training data in the first place. This should be perfectly private (and indeed from the perspective of the learning algorithm it is), but the memorization filter will still cause the system to leak exactly as much information as before. That is, if we prompt the new model $f’$ to output some data that is in the training set, the filter will still kick in and reject the output.

Takeaways

To wrap up, when studying the privacy of a deployed ML application, we have to consider the system as a whole and not just the model in isolation.

Now, this doesn’t necessarily mean that one shouldn’t use components like data deduplication or memorization filters. We just have to be careful about what privacy guarantees we want. If we care about empirically minimizing memorization of training data, then deduplication and memorization filters remain great tools. However, if we care about worst-case privacy guarantees (e.g., against membership inference attacks) then we need to ensure that we our differential privacy guarantees apply to the entire ML system, and not just the training algorithm (and this might mean foregoing some components like memorization filters).