The last decade has seen an impressive rate of progress in machine learning (ML). Fueled by advances in deep learning and computer hardware, the performance of ML models has been steadily improving with some models even achieving superhuman performance in their area of expertise, meaning that they perform better on average than any human does.
However, such systems are by no means perfect and are routinely shown to have robustness and fairness issues. With the advent of superhuman AI systems, finding and fixing such bugs can become increasingly difficult as AI systems develop a better understanding of the ground truth than humans, making it difficult for humans to check whether specific actions/outputs of such a system are correct. In our recent paper, we propose a methodology for evaluating systems when ground truth is unknown.
To illustrate, consider the following two examples:
 |
|
In both cases, the ground truth is not known to us humans. Furthermore, for both problems there either already exist AI systems that perform at a superhuman level (as in the case of chess), or researchers are actively working to get to a superhuman level (as in the case of forecasting). Given that in the future we expect more and more AI systems to achieve superhuman performance in domains with no ground truth, we ask ourselves:
In this post, we show that it is still possible to evaluate superhuman models by making use of consistency checks in the input domain.
Evaluating Superhuman Models with Consistency Checks
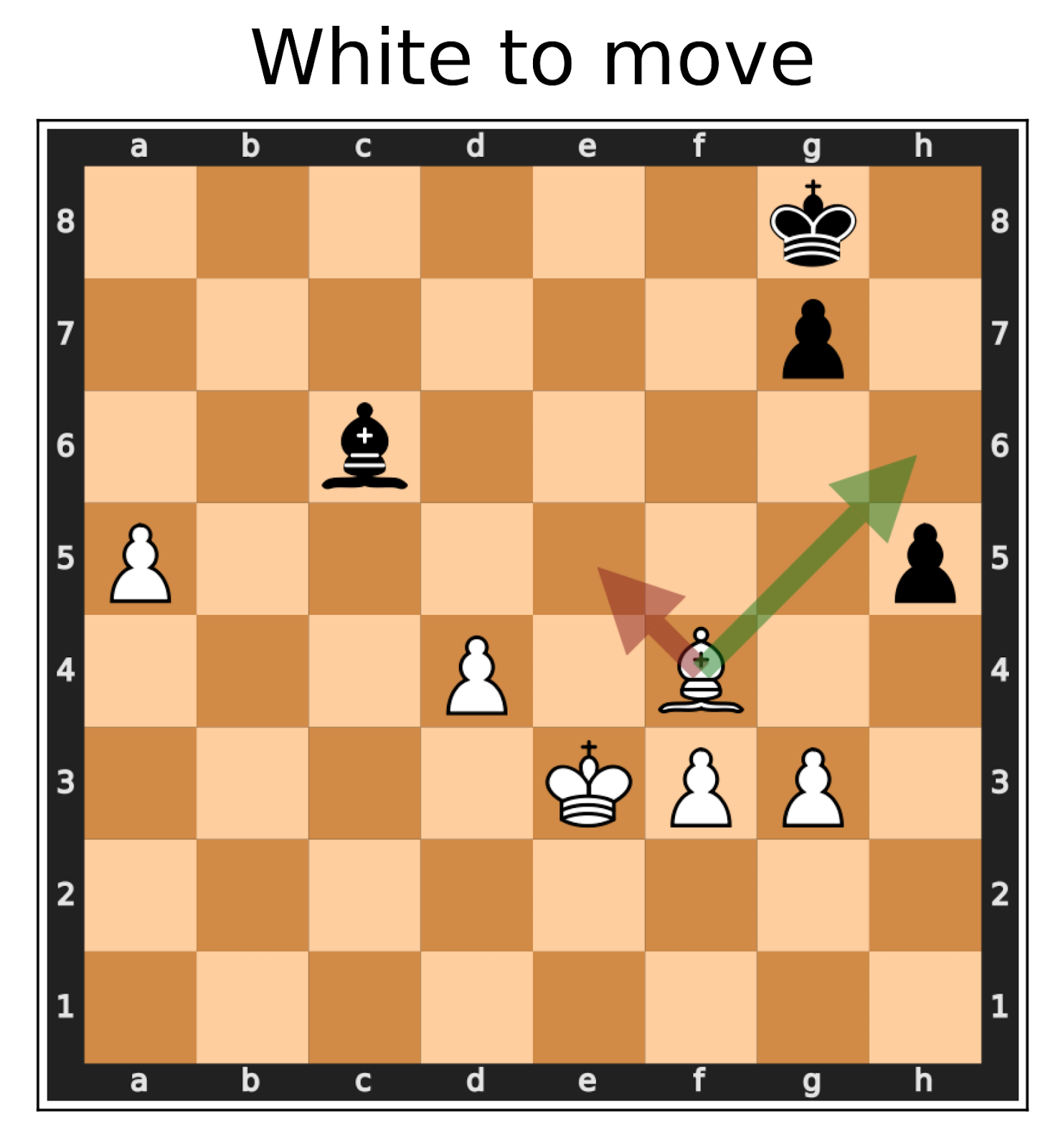
Consider again the Chess example from the introduction. While we do not know whether the proposed move (Bishop to h3) is good or not, we know that if we mirror the board (see the above figure for an explanation), the best move must not change because the two positions are semantically equivalent. If we test our chess AI on this mirrored position and it suddenly proposes some different best move like the one marked with the red arrow, we have found an error, without relying on having access to the ground truth!
 |  |
| The original position. | The transformed position where White gets the piece setup of Black, and vice-versa. |
The right board depicts the left board mirrored over the central horizontal axis. Now, White gets the same position that Black had originally, and vice versa. This means that the best move for Black on the first board should be the mirrored best move for White on the second board.
Related work
This method of testing is not entirely new. Early forms of it have been around since the late 90s, in the form of metamorphic testing which was used to automatically generate test cases for software systems. Various forms of simple consistency checks have also been used to test the robustness of ML models such as image classifiers, or language models (see our paper for a thorough literature overview). In our work, we apply a very general version of this method to evaluate various superhuman and non-superhuman AI systems which operate in domains where the ground truth is unknown.
Evaluating superhuman chess systems
We are interested to see whether this method of using consistency checks to evaluate ML systems is powerful enough to find failures in state-of-the-art, superhuman AI models. We evaluate multiple AI systems which operate in domains where the ground truth is unknown. We start by analyzing a superhuman chess AI. For many chess positions, deciding which side is better off is very hard, and moving a single piece to an adjacent square might completely change the evaluation. Lastly, there exist several superhuman chess AI systems which are open-source and therefore easily accessible.
For our experiments, we test a recent version of Leela Chess Zero, a superhuman chess AI, based on AlphaZero. When analyzing a board position, Leela outputs a value in the interval [-1, 1] representing a continuous approximation of the true game outcome (1 = Win, 0 = Draw, -1 = Loss) for the current player.
In order to find out whether the evaluation of a given board position is correct, we apply several transformations to the original board position which do transform the game outcome in a predictable manner. For example, a transformation could, as in the board mirroring example above, completely flip the winning chances, such that White now has the same winning chances as Black had in the original board position. This allows us to test whether Leela is consistent with respect to said consistency constraints (i.e., in our example, whether the evaluation value of the transformed board is actually the negative of the evaluation value of the original board).
In our experiments, we test Leela on chess positions that occurred during Master-level games. A detailed experiment setup can be found in the paper. We find that in general, Leela is very consistent (as one would expect from a superhuman chess AI). However, we are still able to find multiple large consistency violations, i.e., real game positions where Leela fails to satisfy simple consistency checks:A perfect model would only output values in {-1, 0, 1}, since chess is a deterministic game. However, the continuous approximation of the score (and hence the derived win probability) is the key internal metric used by Leela to decide which move to play, and inconsistencies in this metric indicate clear failures of the model.
 | 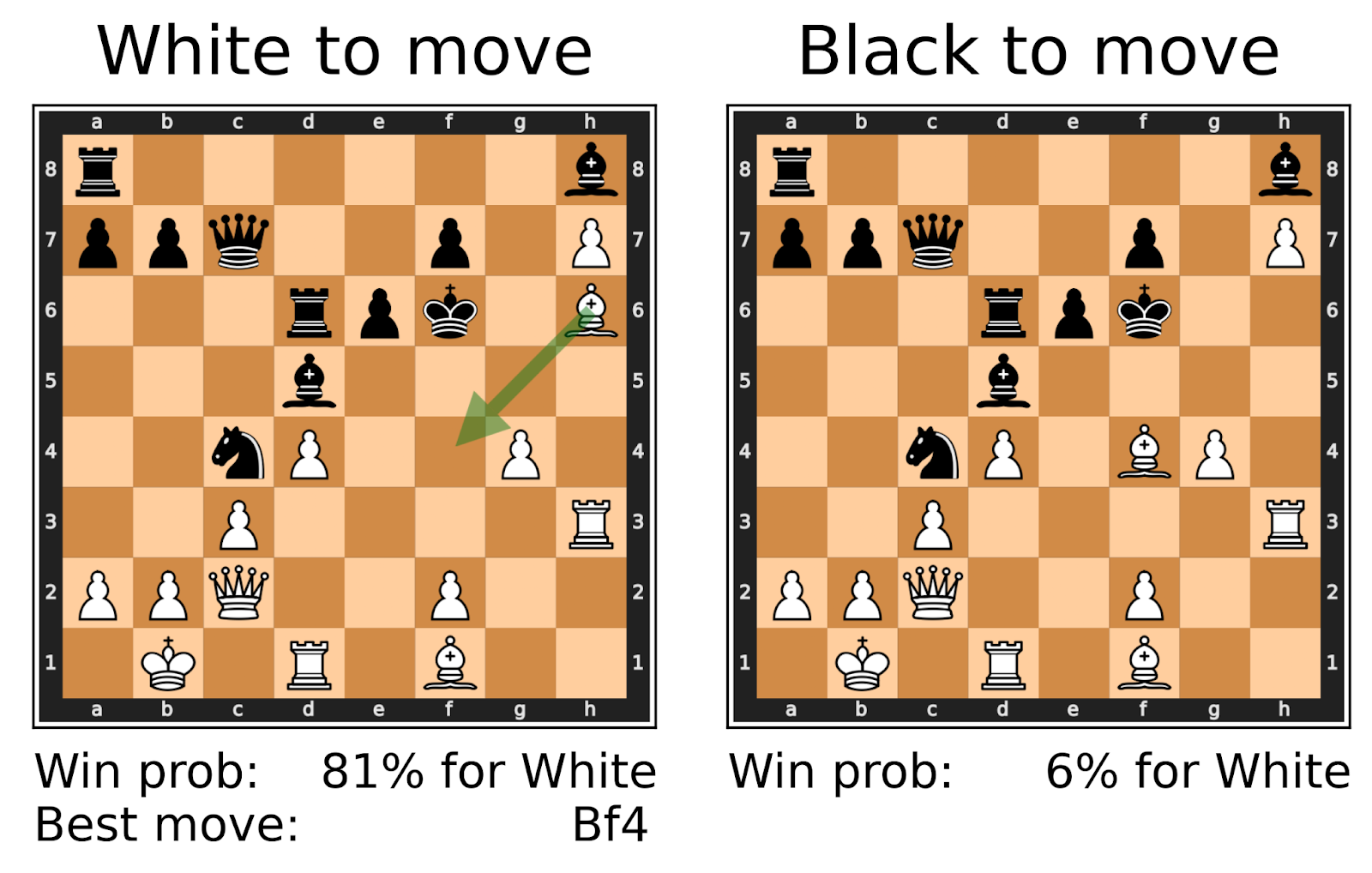 |
| When mirroring a board, the win probability of Black in the first position must be the same as the win probability of White in the second position. However, Leela estimates drastically different probabilities. | An example where Leela blunders. When playing the recommended best move, the estimated winning probability should not change too much. However, Leela Chess Zero only realizes that Bishop f4 is a bad move after playing it. |
 |  |
| When there is only one legal move available, playing that move has no influence on the outcome of the game, and the win probability before- and after playing the move must be equal. However, Leela assigns drastically different win probabilities. | A position without pawns and without castling can be flipped or rotated without changing the evaluation. This is possible because all pieces (except for pawns) can move symmetrically in all four directions. In this example, we rotate the board by 90° counter-clockwise which leads Leela to completely change its mind. |
Beyond Chess AIs: From Forecasting to Legal Assistance
While our evaluation method proved useful for the evaluation of chess AIs, our goal is for our method to be broadly applicable to many different settings beyond chess. In the next step, we, therefore, applied our evaluation method to evaluate language models and legal judgment prediction classifiers. While the evaluated models are not necessarily superhuman, their problem domains do fulfill the two requirements of “hard to verify correctness” and “existence of consistency checks” that are necessary for our evaluation method to be applicable.
Forecasting experiments on GPT-4
Forecasting questions are a good example of a “no ground truth” task. Consider questions like:
- How many people will have been in space by the year 2030?
- What is the probability that Senator X will win the 2028 Republican primaries?
Such questions can be extremely hard to predict before they get resolved. Therefore, it is very hard to evaluate the predictions of an AI system trained to make such forecasts. Consistency checks, however, are readily available to upper bound the model’s forecasting ability. Additionally to asking how many people have been in space by 2030, one could also let the model make predictions for the following questions:
- How many people will have been in space by the year 2025?
- How many people will have been in space by the year 2035?
This is a monotonically increasing series. If the AI system for some reason predicts lower numbers for 2035 than for 2030, we know that its predictions can not be trusted.
Similarly, for the example of the primaries, one can prompt the model to make predictions for the following events:
- What is the probability that Senator X will be elected president in 2028?
- What is the probability that Senator X will not win the 2028 Republican primaries?
Clearly, the probability of being elected president must be smaller or equal to the probability of winning the primaries. And, ideally, the probability of not winning the primaries should sum to 1 when added to the probability of winning the primaries. These easy checks allow us to either gain additional confidence in our model’s predictions or let us expose a model’s bad performance. All of this without knowing the ground truth!
In our experiments, we test GPT-4 on a custom-made dataset of forecasting questions partly derived from the autocast dataset. We show that GPT-4 is a very inconsistent forecaster:
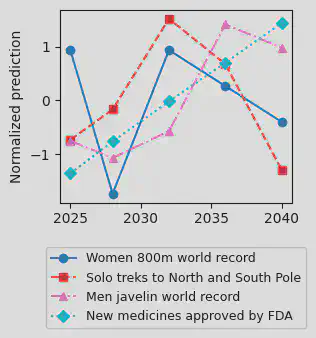 |  |
| The median forecasts of GPT-4 for monotonic quantities are often non-monotonic. The plot shows normalized forecast values of GPT-4 for different monotonic series. | The result of asking GPT-4 to predict probabilities for events and their negation. Ideally we have P(event) = 1 - P(¬event). However, the plot shows several large outliers. |
Compared to GPT-3.5-turbo, GPT-4 revealed a clear improvement in consistency, except on our most complex consistency constraint which checked Bayes’ rule. This consistency constraint takes two events A and B, and then checks whether GPT-X’s predictions for P(A), P(B), P(A|B) and P(B|A) violate Bayes’ theorem. We found this to be true more than 50% of the time. This indicates that more involved consistency checks could remain a reliable way of surfacing model failures, even if model abilities improve drastically in the future.
Legal decisions
Lastly, we also look at several problems in the legal domain. Reaching decisions on complex legal cases can be long and costly, and the “correctness” of decisions is often contested (e.g., as evidenced by appeal courts). The difficulties in assessing the correctness or fairness of human legal decisions have led to a flurry of AI tools that are used to assist or automate legal decisions. In this section, we show how to reveal clear logical inconsistencies in two different language models used for predicting legal verdicts.
First, we use GPT-3.5-turbo to predict whether an arrested individual should be released on bail, given their criminal history. The queried cases represent real legal cases that have been extracted from the COMPAS dataset. Although we are not able to determine the real optimal decision, we are still able to test GPT by testing moral consistencies, like the fact that more previous crimes should not increase the likelihood to receive bail. Nevertheless, we are able to find several examples where GPT-3.5-turbo violates this consistency:
 |
| A legal case where GPT-3.5-turbo does not offer bail if the defendant committed one prior crime, but does offer bail when the exact same defendant committed two prior crimes. |
In a second experiment, we evaluate a BERT model, which has been specifically trained to predict violations of the European Convention of Human Rights. The model is a close adaption of Chalkidis et al’s LEGAL-BERT model. Given a legal case, consisting of a list of individual case facts, we paraphrase a single case fact and let the BERT model predict, whether the two legal cases (the original and the one with a single paraphrased fact) describe a violation of the European Convention of Human Rights. Note that it is clearly difficult for humans to decide this, because a legal case must go through multiple lower-level courts in order to be tried in front of the European Court of Human Rights. Yet, we are again able to find multiple legal cases, where paraphrasing a single fact leads to the model changing its mind:
 |
| An example legal case where paraphrasing a fact makes the model change its prediction from “Law violated” to “No Law violated”. Text removed by the paraphrasing process is depicted in red, whereas text added by the paraphrasing process is shown in green. Note that the paraphrasing merely changed the case fact’s syntax, but not its meaning. |
The legal experiments demonstrate certain alignment failures: If an AI is inconsistent in this way on counterfactual cases, it means it fails to robustly encode human values.
Finding consistency failures more efficiently
As AI systems get smarter, consistency failures become rarer. Therefore, at a certain point randomly sampling inputs to find consistency violations might become infeasible. So, does our method become useless with increasing model performance? We claim that not all hope is lost. There are several ways to search for consistency violations in a smarter way than random sampling, which manage to drastically increase the efficiency of our method.
Black-box directed search
One of the advantages of our method is that it only requires black-box access to the model under evaluation. It would be preferable to preserve this property since many state-of-the-art models are only accessible through APIs. Therefore, we first experiment with using a black-box directed search to find input samples for which our model under evaluation violates consistency constraints. In particular, we develop a genetic algorithm that randomly mutates and mates a population of input samples in order to find input samples with a high probability of eliciting consistency failures.
We test our directed search by evaluating a particularly strong instance of Leela and are able to find up to 30x more strong consistency failures than with a simple black-box search:
| Number of strong consistency violations found (out of 50k) | |
| Randomly sampling inputs | 7 |
| Directed black-box search | 209 |
White-box directed search
A much more effective approach is to discard the black-box property and exploit the model’s internals to find input samples which violate consistency constraints. Gradients, in particular, are a valuable tool for finding adversarial examples. We show that even weaker models of white-box access are already very useful to find consistency violations more efficiently.
In particular, we increase the efficiency of finding consistency violations in our LEGAL-BERT model, used to predict violations of the European Convention of Human Rights (see the previous section). This BERT model uses a self-attention layer to assign an importance weight to each individual case fact. This allows us to quickly find the most important case fact (according to the model). By paraphrasing this fact in particular, instead of some random case fact from the case, we are able to greatly increase the probability of finding consistency failures in this model:
 |  |
| A scatter plot depicting the probability that a given legal case and a randomly paraphrased version of it contain a violation of the European Convention of Human Rights. Red points represent cases where the model actually flipped its prediction from “No law violated” to “Law violated” and vice versa. | A scatter plot depicting the probability that a given legal case and a version where we specifically paraphrase the most important case fact contain a violation of the European Convention of Human Rights. Red points represent cases where the model actually flipped its prediction from “No law violated” to “Law violated” and vice versa. |
Limitations and Extensions
While we have succeeded in demonstrating clear logical consistency violations in a variety of settings and models, our current approach has limitations that we hope future work can address.
First, some inconsistencies we find are rare, especially for superhuman models such as Leela.
One reason is that we mainly search for bugs in a black-box manner with random sampling. As we have shown for both chess evaluations and legal decisions, a white-box adversarial search reveals many more violations. As models become stronger (and exhibit superhuman abilities on tasks beyond games), consistency bugs may be so rare that they can only be discovered by adversarially guided search.
Second, while we focus on “hard” consistency constraints (i.e., which should always logically hold), our experiments sometimes use automated tools to generate (pseudo)-consistent tuples (e.g., via paraphrasing). While we manually checked these, it is possible that we missed some unsound checks. Again, as models become better and bugs rarer, relaxing soundness may be necessary in order to get checks with better completeness. Discovered bugs would then have to be further vetted by humans or trustworthy models. Concurrent work has explored multi-turn cross-examination (as proposed in Barnes & Christiano) to elicit “soft” inconsistencies, although in settings where the ground truth is available. We leave it to future work to explore ways to automate and scale this process to superhuman models.
Finally, as for any (incomplete) technique for discovering bugs, finding nothing does not mean an absence of bugs! While violations of our consistency checks are a clear sign that a model’s correctness cannot be trusted for high-stakes settings, this does not imply that future, better models that pass simple consistency checks should be absolutely trusted.
Conclusion
In this project, we tackled the question of how to evaluate superhuman AI systems in the absence of ground truth. We developed an evaluation framework based on metamorphic testing, which allows us to perform black-box evaluations of potentially superhuman AI systems. The framework tests the model under evaluation by verifying whether the model complies with consistency constraints imposed by the problem domain.
Future work could further look into the question of how to find inconsistencies when they are rare. One potential solution is to employ white-box, adversarial methods such as gradient descent that have already been shown to be a valuable tool for finding adversarial examples. One downside of using such methods, however, is losing the advantages of having a completely black-box approach without any reliance on the inner workings of the system under test.
